區塊鏈中的 Merkle Tree：加密資料儲存深度解析

區塊鏈網路快速成長，帶來資料儲存與管理上的重大挑戰。隨著加密貨幣交易量不斷累積，節點維護完整交易紀錄的壓力也持續增加。這種擴張不僅影響區塊鏈的安全性、透明度與去中心化原則，同時對高效解決方案提出更嚴苛要求。Merkle Tree 是密碼學領域的重要創新，已成為解決這些問題的關鍵技術，為區塊鏈資料的有序組織與高效驗證提供優雅解方，並維護網路的整體完整性。

加密領域中的 Merkle Tree 是什麼？

Merkle Tree（雜湊樹）是一種專為加密貨幣區塊鏈網路設計的資料結構，用於組織、匯總及加密交易資料。該概念由電腦科學家 Ralph Merkle 於 1979 年提出且申請專利，自此成為區塊鏈架構不可或缺的核心技術，是加密網路資訊處理與排列的基石。

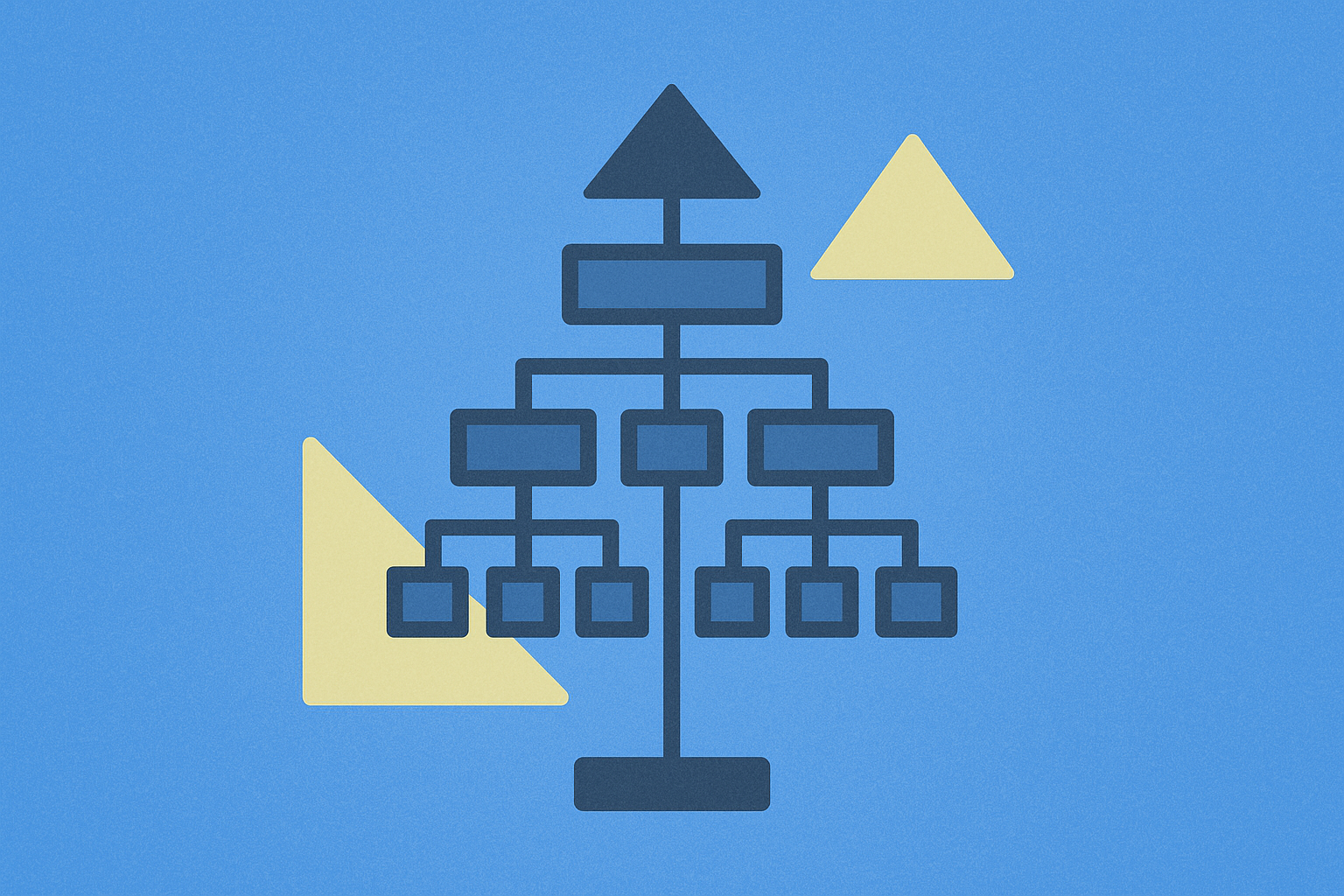
Merkle Tree 採樹狀分層結構，包含三大核心組成：Merkle 根、Merkle 分支和 Merkle 葉。葉節點作為基底，儲存每筆交易的唯一識別；分支位於中間層，匯總葉節點的交易資料；最上層則為 Merkle 根，集中整合區塊內所有交易資訊。

這種分層架構實現高效資料壓縮。Merkle 根作為所有底層交易資料的唯一代表，顯著減少節點記憶體需求。節點僅需保留根值即可維持區塊鏈完整性，無須保存每筆交易細節。同時，這樣的組織方式大幅提升資料可存取性，讓節點營運者及加密貨幣交易者能快速檢索及精確定位交易紀錄。

Merkle Tree 在區塊鏈中的運作原理

要理解 Merkle Tree 及其運作方式，須先認識密碼學雜湊函數，這是其技術基礎。密碼學雜湊函數屬於不可逆的單向演算法，能將數位資料轉換為唯一且固定長度的字串（雜湊值），就像給輸入資料蓋上獨一無二的「指紋」。在加密貨幣領域，輸入值代表區塊鏈上的交易，透過雜湊演算法確保每筆加密轉帳擁有唯一雜湊值。

Merkle Tree 仰賴雜湊函數的可靠性與確定性，自底向上匯總交易資料。區塊鏈會為每筆獨立交易產生雜湊值，形成 Merkle 葉節點。接著，演算法將葉節點兩兩配對，透過雜湊函數產生新的分支雜湊值。此過程層層遞進，分支持續合併至更高層，最終產生唯一的 Merkle 根雜湊值，完整加密代表區塊內所有交易。

舉例來說，若一個區塊包含 8 筆交易，Merkle Tree 會先產生 8 個葉節點雜湊，然後兩兩配對雜湊為 4 個分支雜湊，再合併成 2 個更高層分支，最終匯聚成 1 個 Merkle 根。這項數學設計不僅確保資料完整性，也大幅減少儲存需求——整個交易紀錄皆可透過單一根雜湊值驗證。

Merkle Tree 在區塊鏈中的優勢

深入了解 Merkle Tree，需認識其為加密貨幣網路帶來的多重優勢：不僅資料壓縮效果顯著，更大幅提升運作效率與安全性，是區塊鏈可持續擴展的核心技術。

其最大優勢在於能為大規模資料集建立高度緊湊的檔案。每個 Merkle 根雜湊都是區塊內多筆交易的完整加密表示，顯著降低儲存與共享網路活動紀錄所需空間。資料負載減輕，節點營運硬體門檻降低，讓更多個人與機構可參與驗證節點營運，直接強化網路的去中心化、可擴展性與整體效率。這對於區塊鏈分散式特性至關重要，特別是在交易量快速成長時。

Merkle Tree 同時具備強大防竄改能力。雜湊值間的密碼學關聯建立起不可變的資料結構，每個雜湊值與其前序交易值有數學關聯，任何竄改葉節點、分支或根都會造成全網可偵測的變化，幾乎不可能被隱匿。複雜的加密關係讓節點能即時察覺資料遭竄改的跡象，確保網路完整性與正確運作。

此外，Merkle Tree 倚賴雜湊函數的碰撞抗性進一步提升安全性。碰撞抗性能確保幾乎不可能出現兩筆不同資料卻有相同雜湊輸出，進而保證 Merkle Tree 內所有資料都擁有唯一、可加密驗證的識別，有效防止偽造與未經授權的修改。

Merkle Tree 儲備證明是什麼？

Merkle Tree 除了在區塊鏈交易處理（如比特幣網路）中扮演關鍵角色，也廣泛應用於金融透明與驗證領域。儲備證明（PoR）正是一項重要實踐，應用於加密貨幣交易平台與去中心化應用（dApp）的財務可驗證性。

儲備證明是一種透明報告機制，揭露加密貨幣業者或 Web3 協議的資產與負債，為利害關係人提供可驗證的償付能力證據。交易平台以每個客戶帳戶資料為葉節點建立 Merkle Tree，逐層匯總至分支，最終產生代表所有負債的 Merkle 根。雜湊函數的防竄改特性使第三方審計師能高效驗證 PoR 聲明的有效性，確認所申報資產足以覆蓋當前負債。

此方法同時為加密貨幣交易者及客戶帶來額外好處。Merkle Tree 的透明架構允許用戶自行識別並驗證自身交易或帳戶葉節點，無需接觸其他用戶的隱私資訊。雖然交易平台會以定期餘額截圖等多種方式展示 PoR，然而 Merkle Tree 憑藉數學透明性、密碼學安全性與去中介化優勢，已成業界標準。

Merkle Tree 與 Verkle Tree 的差異

區塊鏈資料結構持續演進，Verkle Tree 的創新推動可擴展性進一步突破傳統 Merkle Tree。比較兩者，電腦科學家 John Kuszmaul 於 2018 年提出 Verkle Tree，帶來進一步降低頻寬需求、提升網路效率的新方案。

Merkle Tree 與 Verkle Tree 的核心差異在於底層密碼學機制。Merkle Tree 採用密碼學雜湊函數連結葉節點和分支，而 Verkle Tree 則引入向量承諾（vector commitments）作為分支加密機制。這項變革能讓節點驗證交易有效性時，將所需資料量降至最低。在 Verkle Tree 模式下，節點僅需檢查較小的加密證明，無需像傳統 Merkle Tree 那樣遍歷整棵樹的雜湊值。

Verkle Tree 有望大幅提升區塊鏈可擴展性，吸引以太坊等主流專案關注，並納入未來升級提案。不過，該技術仍屬加密領域的實驗階段，部署複雜，需持續研究、測試與實際應用，開發者才能全面評估其真正優勢與限制。加密社群普遍認為，持續開發與驗證是確定 Verkle Tree 在區塊鏈生產環境可行性及最佳應用場景的關鍵。

總結

Merkle Tree 是區塊鏈技術的基礎創新，解決資料儲存、驗證和擴展等核心問題。透過葉、分支與根的分層結構，Merkle Tree 實現大規模交易資料的高效壓縮，同時維護密碼學安全與完整性。其緊湊的資料表示、防竄改檢測與碰撞抗性等優勢，使其成為比特幣、以太坊等加密網路以及儲備證明等應用的關鍵技術。

隨著區塊鏈技術持續演進，Merkle Tree 仍穩居推動去中心化與網路可及性的核心地位。新世代結構如 Verkle Tree 的出現，彰顯產業對區塊鏈效率持續優化的努力，而傳統 Merkle Tree 也透過長期實踐證明其可靠與高效。深入理解 Merkle Tree 的原理，是掌握現代加密貨幣網路安全、透明與可擴展技術基礎的關鍵。其數學設計展現密碼學創新在維持去中心化原則下，解決現實複雜挑戰的巨大價值。

常見問題

Merkle 的含義是什麼？

Merkle 是德語姓氏，原意為「邊境守衛」。在加密領域，Merkle 通常指涉區塊鏈技術中的關鍵資料結構——Merkle Tree。

Merkle 的用途有哪些？

Merkle Tree 可用於分散式系統中的高效資料驗證與同步，確保資料完整性與一致性。

Merkle Tree 與雜湊樹有何不同？

Merkle Tree 與雜湊樹在密碼學領域本質相同，都是透過雜湊函數構建分層結構，以實現高效資料驗證與完整性校驗。